Many people are familiar with Newton’s Laws of motion. While you may not be able to describe them in a scientifically precise way, you probably know what they are and what they mean for physics. In the world of astronomy, there are three very similar laws that dictate how physics works in space; Kepler’s Laws.
To be honest, Kepler’s Laws actually apply everywhere you have a central force (like gravity!) and conservation of angular momentum. They are just three concise ways of describing the effect of this force. However they are most applicable to astronomy when considering orbital motions so I’ll stay within that context.
First a little bit about Kepler to get you interested:
Johannes Kepler [December 27, 1571 – November 15, 1630] lived around the same time as Galileo. He was a German mathematician, astronomer and astrologer. At the time, the definition between astronomy and astrology was a bit hazy – but the difference between astronomy and physics was quite distinct. His laws were products of his work in astronomy as he set out to describe Mars’ orbit fully. He tried to use an oval shape, but after 40 failed attempts, realized that an ellipse would work better! Ultimately his work in astronomy was not well received due to the fact that he had merged astronomy and physics. However after his death, when Isaac Newton eventually described the same laws of motion using his gravitational mechanics, Kepler’s contribution to astronomy was recognized for how influential it was.
Kepler’s first law describes the shape of a planet’s orbit. In studying the motion of the planets, Kepler concluded that orbits are ellipses, with varying degrees of eccentricity – or “stretched out-ness”. Ellipses are described by two lengths; the semi major axis and the semi minor axis. The former describes the size of the longer dimension of the ellipse, while the later is the shorter dimension. The size of a planet’s orbit is often described with the semi-major axis.
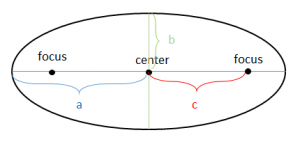
Kepler’s second law describes the speed of the planet as it orbits. In order to conserve energy, as a planet moves around it’s star, the speed must be related to how far away the planet is from the star. One way to get a feel for this is to imagine swinging a ball attached to a string above your head. If you use a small amount of string, you have to swing the ball quite quickly to make it continue around in a circle without hitting your head. However, if you use a large amount of string, you do not have to swing the ball as fast. In fact, the ball moves much slower in this case.
The same thing happens with a planet as it moves around it’s star. When the planet is closest to the sun (this is called perihelion), it is moving fastest. When the planet is far away from the sun (aphelion) it is moving slower.
Finally Kepler’s third law describes a relationship between the period of the orbit, or time it takes to make one full orbit, and the semi-major axis (remember this is a descriptor for how large the orbit is). Algebraically, it can be written
P^2 ~ a^3
where P is the period of the orbit and a is the semi-major axis [~ implies ‘proportional to’]. This relation tells you that the period is related to the size of the orbit, or that the size of the orbit effects how long it takes for the planet to make one full revolution. While this may seem to be intuitive, it is remarkable that this relationship could be described so succinctly and still apply to all of the planets. Is wasn’t until 1687 that Newton would derive this relationship using his theory of gravitation, however it is currently easiest to work from Newton’s ideas back to Kepler’s third Law.
First we will define two things; the force on an object due to gravity:
F = GMm/r^2
where G is the gravitational constant, M the mass of the star, m the mass of the planet and r the semi major axis, and the acceleration of an object moving in a circle:
a = v^2/r
where v is the velocity of the planet. Newton’s second law tells us that the total force on an object can be described as the mass, m, times the total acceleration, a. [sorry for the double definition of acceleration and semi-major axis, from now one the semi major axis will be r] If we assume that the only force is gravity and write the acceleration as above we have
F = ma
GMm/r^2 = m(v^2/r)
With some canceling and algebraic rearranging we find
GM/v^2 = r
Now what is the velocity of a planet? If we assume it travels in a circle (while contrary to Kepler’s first law, it works as an approximation), the full distance the planet travels would be the circumference of that circle: 2 [pi] r and the time it takes to go around the star completely is the period, P. Using this the velocity can be written as
v = 2[pi] r/P
Now we can insert this into the equation above and rearrange to find
(GM/4[pi]^2 ) P^2 = r^3
or since (GM/4[pi]^2 ) is just a constant,
P^2 ~ r^3
So, by looking at the force of gravity on a planet as it orbits the Sun, we were able to derive the same relationship that Kepler derived from studying the motions of the planets.
That’s it for Kepler’s laws. I’ll leave you with another fun fact about Kepler; in an episode of Cosmos, Carl Sagan described Kepler as “the first astrophysicist and the last scientific astrologer”.
It’s a bit sad how many creative thinkers and scientists were dismissed when they were alive, only to later be recognized for their contributions.
I had visions of us swinging a tennis ball sized planet around our heads. I imagined you with the short string… 🙂 Excellent example.
You had me right up until the word “Algebraically”…. at which point I simply appreciated how very smart you are, and reflected on my most hated Jr. High School teacher – Mrs. Ransom, who would poke her finger into my shoulder and shove a garbage can in my face if I forgot to spit my gum out BEFOFE class. Yes, she taught algebra and my brain has rejected attempting to comprehend algebraic formulas ever since….
You are smart. 🙂
O God, math! It’s too late to crunch my brain right now. And there was no alert, like a spoiler alert or a trigger warning. Aaaaack. Sleep will hopefully be my Sancho Panza in this upcoming Battle of Comprehension. Lovely illos!
is the earth’s orbit also an ellipse? If so, are we on the short axis in winter or summer? I’m gonna guess shorter in the summer and that’s why it’s so damn hot in Arizona…..
Maybe I’ll do a post on the seasons next… 🙂
Please reread Allison’s comments 😊They describe my thoughts exactly. ( minus Mrs. Ransom) and double the SMART part !